二叉树
树
定义
树(Tree),是一个具有n个节点的有限集,当 n=0 的时候称为空树。
在任意一颗非空树中:
- 有且仅有一个特定地称为根(Root)的结点。
- 当 n>1 的时候,其余结点可以分为m个互不相交的有限集。
当 n>0 的时候,根节点是唯一的,不可能存在多个根节点,数据结构中的树只能有一个根结点。 m>0 的时候,子树的个数没有限制,但是它们一定是互不相交的。
结点是数据结构中的基础,是构成复杂数据结构的基本组成单位。
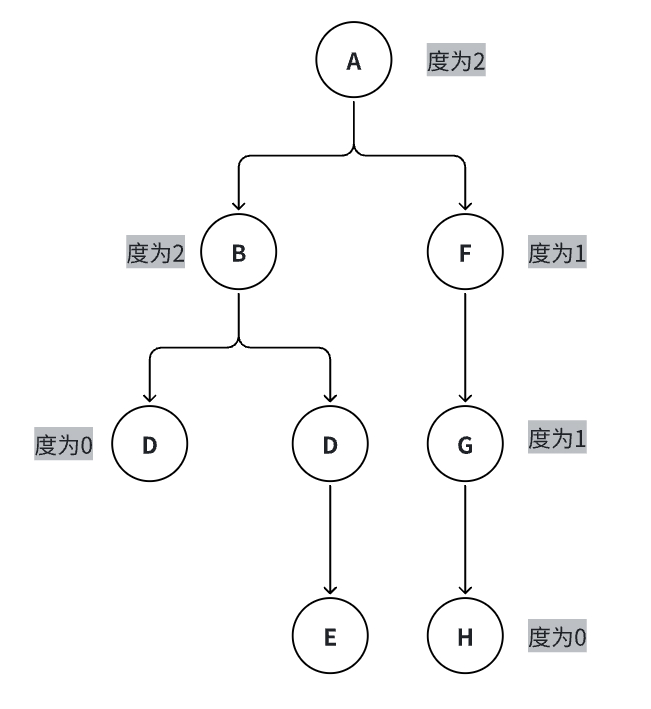
节点的度
结点拥有的子树数目称为结点的度。
结点关系
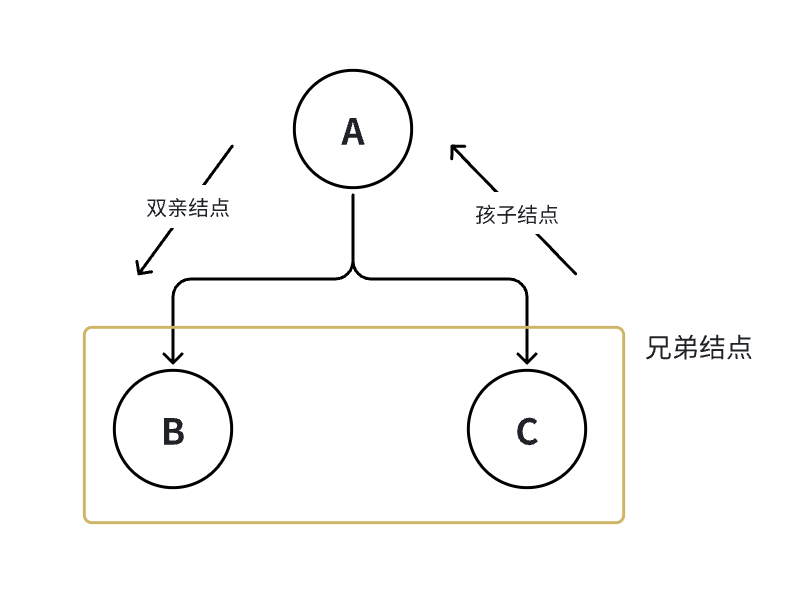
结点子树的的根结点称为该结点的孩子结点,相应的该节点称为孩子结点的双亲结点。同一个双亲结点下的孩子结点之间互称兄弟结点。
A为B和C的双亲结点,B和C为A的孩子结点。
B与C互相为兄弟结点。
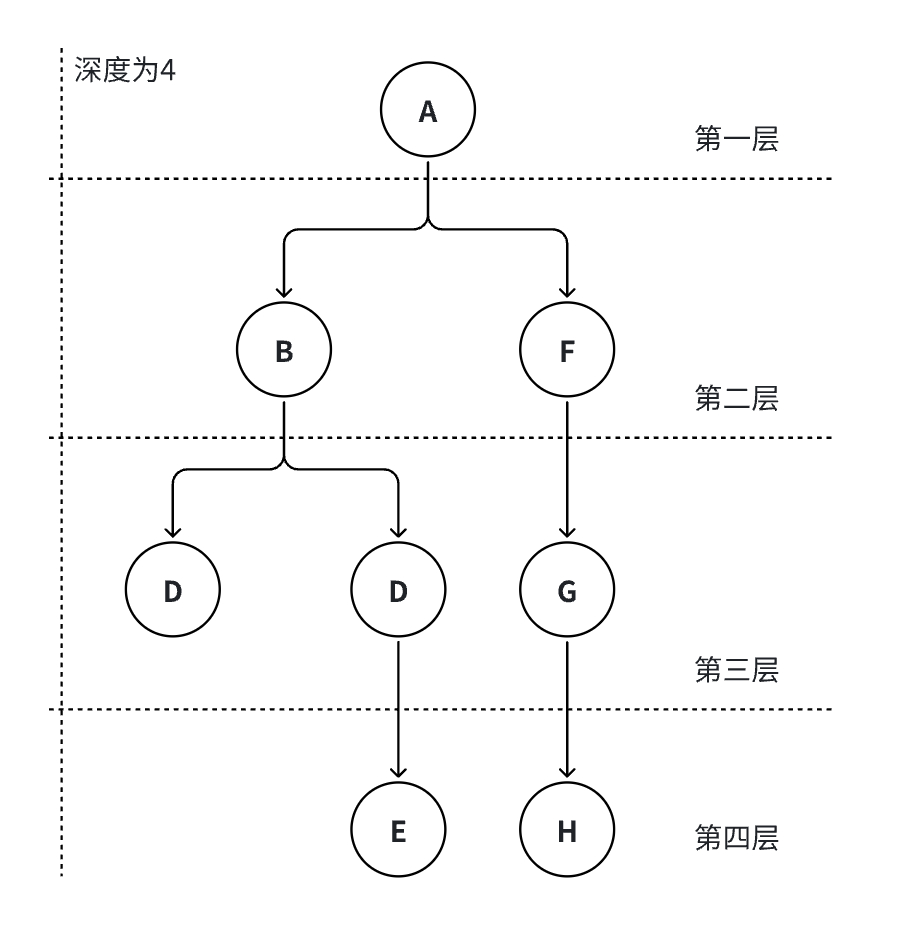
结点层次、树的深度
从根开始定义为第一层,依次类推,树中结点的最大层次称为树的深度或者高度。
二叉树
二叉树是n个结点的有限集合,该集合或者为空集(空二叉树),或者由一个根结点和两颗互不相交的,分别称为根节点的左子树和右子树组成。
二叉树的特点
由于二叉树定义以及相关图示分析出二叉树有如下特点:
- 每个结点最多有两颗子树,所以二叉树中不存在度大于2的结点。
- 左子树和右子树是有顺序的,次序也不能任意颠倒。
- 即使树中某结点只有一颗子树,也要区分它是左子树或者是右子树。
由此可知二叉树有如下性质: